Cs = 0.57/8 = 0.071
< 0.37/{0.36(8)} = 0.13
> 0.044(0.57) = 0.025
Therefore; Cs,long W = 0.095(129k) = 12.2k (54.3KN), Cs,transW = 0.071(129k) = 9.1k (40.5KN)
B-4 Calculate Vertical Distribution of Forces.
Note: The building will behave as two separate structures. In the transverse direction, the single story
structure will distribute some tributary loads to the common lateral load resisting moment frame at the
interface with the two-story structure, but will otherwise behave independently in this direction. In the
longitudinal direction, the single story and two story structures are completely independent due to the
elongated slotted holes in their adjoining connection. Therefore the two structures will be analyzed
independently of each other.
Divide the base shear between the single story and the two story structures
The base shear will be divided between the structures based on the ratio of their masses;
Single story weight = 26.1k (116.1KN)
Two story weight = 19.8k+82.2k = 102k (453.7KN)
Therefore;
Base shear for the single story building;
26.1k
(9.1k ) = 1.9 k (8.45KN)
Vsingle story, trans =
k
128
26.1k
(12.2 k ) = 2.5k (11.12KN)
Vsingle story, long =
128k
Base shear for the two-story building;
102 k
(9.1k ) = 7.2 k (32.03KN)
Vtwo story,trans =
k
128
102 k
(12.2 k ) = 9.7 k (43.15KN)
Vtwo story, long =
k
128
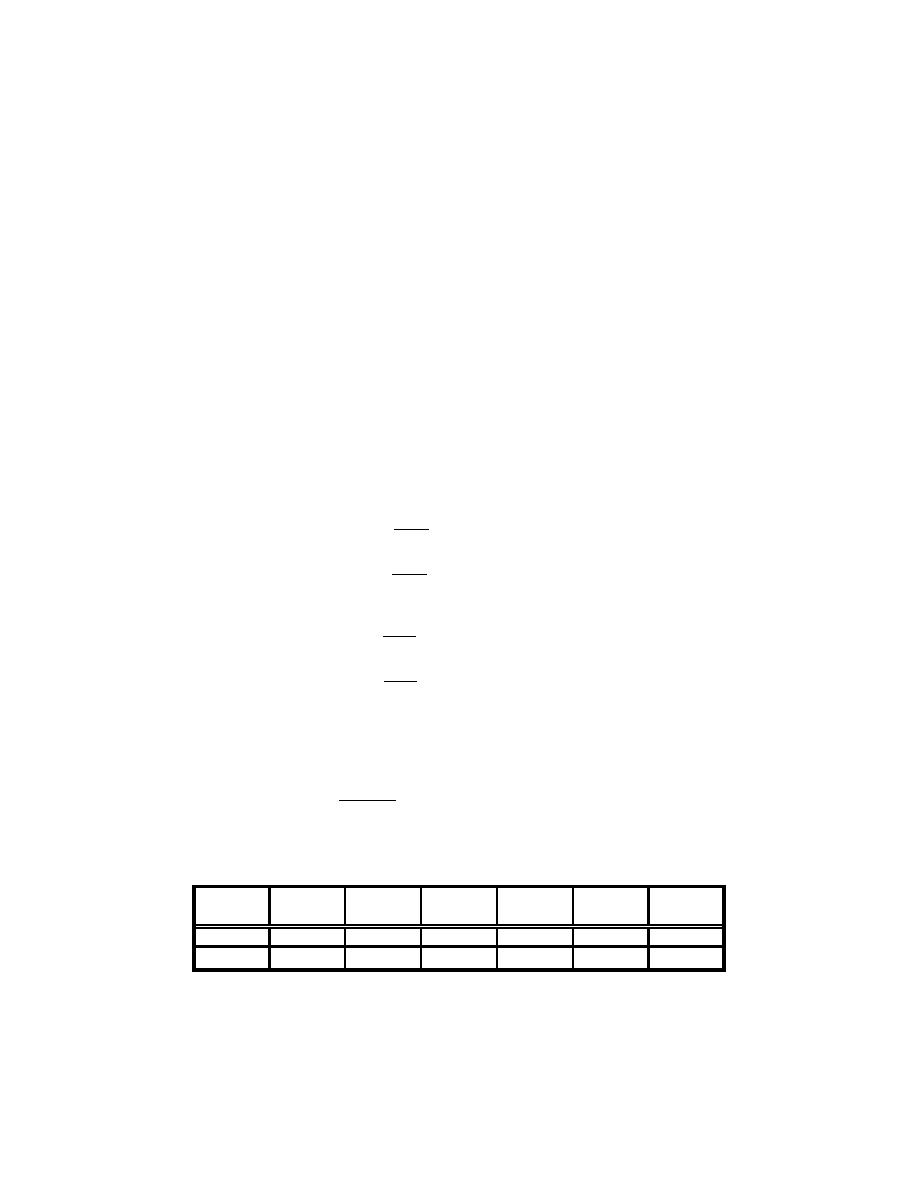
Calculate vertical distribution on two story structure;
Fx = Cvx V
(EQ. 5.3.4-1 FEMA 302)
w xhk
x
C vx =
(EQ. 5.3.4-2 FEMA 302)
n
∑wh
k
ii
i=1
where; k = 1 in both directions for the building period is less than 0.5 sec.
The calculations are tabularized below*;
Story
wi
hi
wixhi
Cvx
CvxxVt
CvxxVL
(kips)
(ft)
(ft-kips)
(kips)
(kips)
Roof
19.8
22
435.6
0.33
2.34
3.15
2nd
82.2
11
904.2
0.67
4.86
6.55
SUM =
102
1339.8
1.00
7.20
9.70
Note: For metric equivalent; 1-kip = 4.448KN, 1-ft = 0.30m, 1-ft-kip = 1.36KN-m
Therefore;
Transverse direction;
Longitudinal direction;
k
Froof = 3.15k (14.01KN)
Froof = 2.34 (10.41KN)
F2nd = 4.86k (21.62KN)
F2nd = 6.55k (29.13KN)
H4-9



 Previous Page
Previous Page
