∆ c( 10.ft ,10.ft )
∆ solid
∆ solid = 0.0003 in
Solid wall ABCD
∆ f( 8.ft ,10.ft )
∆ bcd
∆ bcd = 0.0001 in
Subtract strip BCD
∆a
∆ solid
∆ bcd
∆ a = 0.0002 in
1
R f( 8.ft ,3.33.ft )
R b = 1017.8097
Add back in piers B and C
Rb
in
1
R c = 1017.8097
Rc
Rb
in
1
∆ bc
∆ bc = 0.0005 in
Rb
Rc
∆ total
∆a
∆ bc
∆ total = 0.0007 in
1.kip
kip
KN
R wall = 1449.6
R wall = 253.9
Rigidity of wall
R wall
∆ total
in
mm
For each sacristy;
Shear force tributary to each sacristy = 5.3 kips (23.6 KN)
R element
Velement = V
RA7-A8 = 2448 kips / in
RC7-C8 = 1450 kips /in
∑R
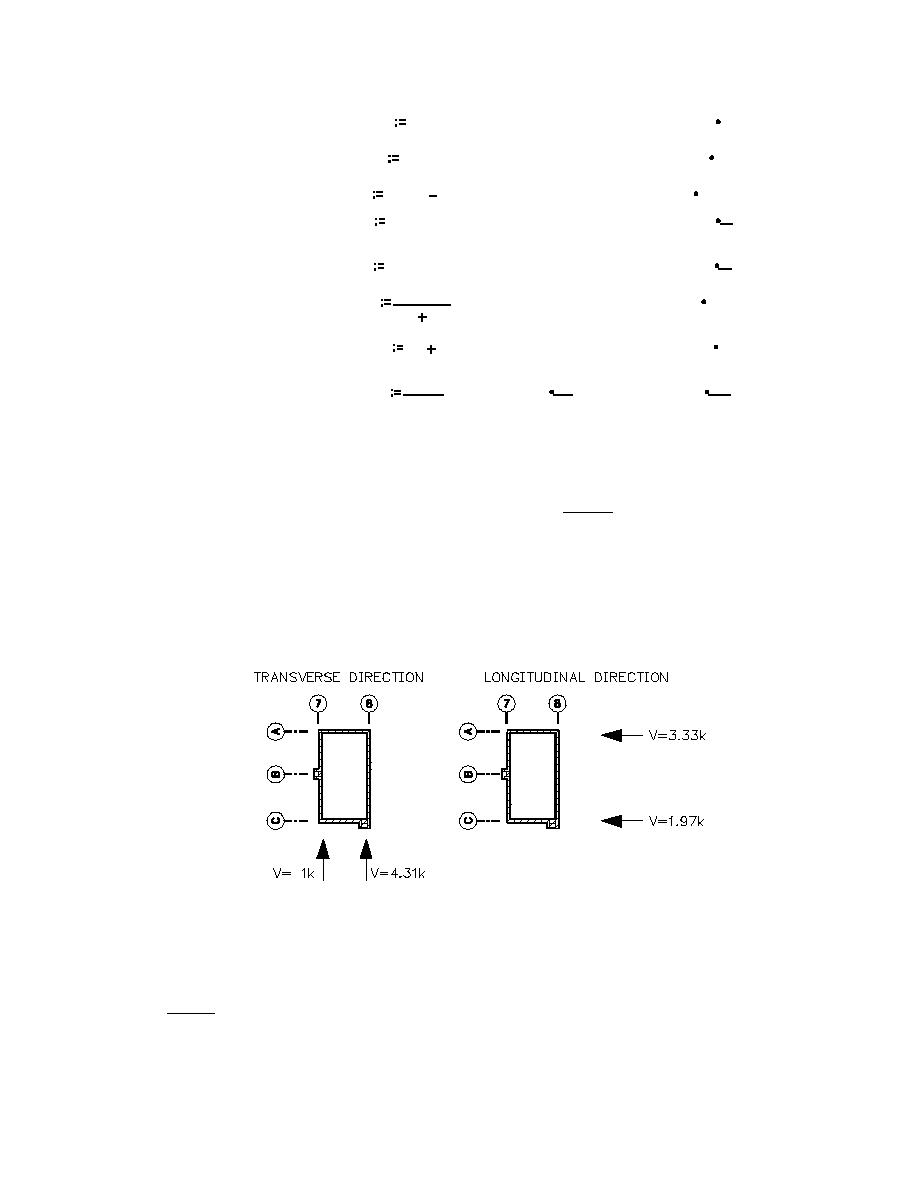
VA7-A8 = 5.3(2448) / (2448 + 1450) = 3.33 kips (14.8 KN)
VC7-C8= 5.3(1450)/(2448+1450) = 1.97 kips (8.76 KN)
Due to symmetry, VI7-I8 = VA7-A8 = 3.33 kips (14.8 KN) VG7-G8 = VC7-C8 = 1.97 kips (8.97 KN)
1 kip = 4.448 KN
B-6 Determine cr and cm
The sacristy and lower sloped roof areas have rigid diaphragms. The torsional forces to the vertical
resisting elements are calculated by finding the tributary mass and stiffness eccentricities.
Sacristy
Center of Mass
H3-31



 Previous Page
Previous Page
