(665psi)(0.32)(0.89)(40)(3.81) 2
=
= 4.58kipft = 54.98kipin (6.21 KNm) > 33.6kipin (3.8 KNm) , OK
M rm
2(12)
FEMA 302 Section 11.10.1 requires that the nominal flexural strength of the wall for out-of-plane flexure
previously to be 28.52 kipin. The flexural strength of the wall determined by allowable stress design was
calculated as 47.7 kipin > 37.1 kipin (= 1.3 x 28.52). The flexural strength of the wall calculated using
ultimate strength design is much greater than the strength calculated from allowable stresses. Therefore,
assume OK.
Out-of-plane shear strength check
-
Shear force demand;
The out-of-plane shear force demand is determined from the horizontal force on the wall face of 16.4
psf. Wall E1-E2 is the most critical with an unbraced span of 20' Therefore, the shear demand for a
.
40" wide section is:
f = wL/2 = (16.4 psf)(40")(1 ft. / 12")(20 ft. / 2) = 547 lb / 40" (2.39 KN/m)
1 inch = 25.4 mm
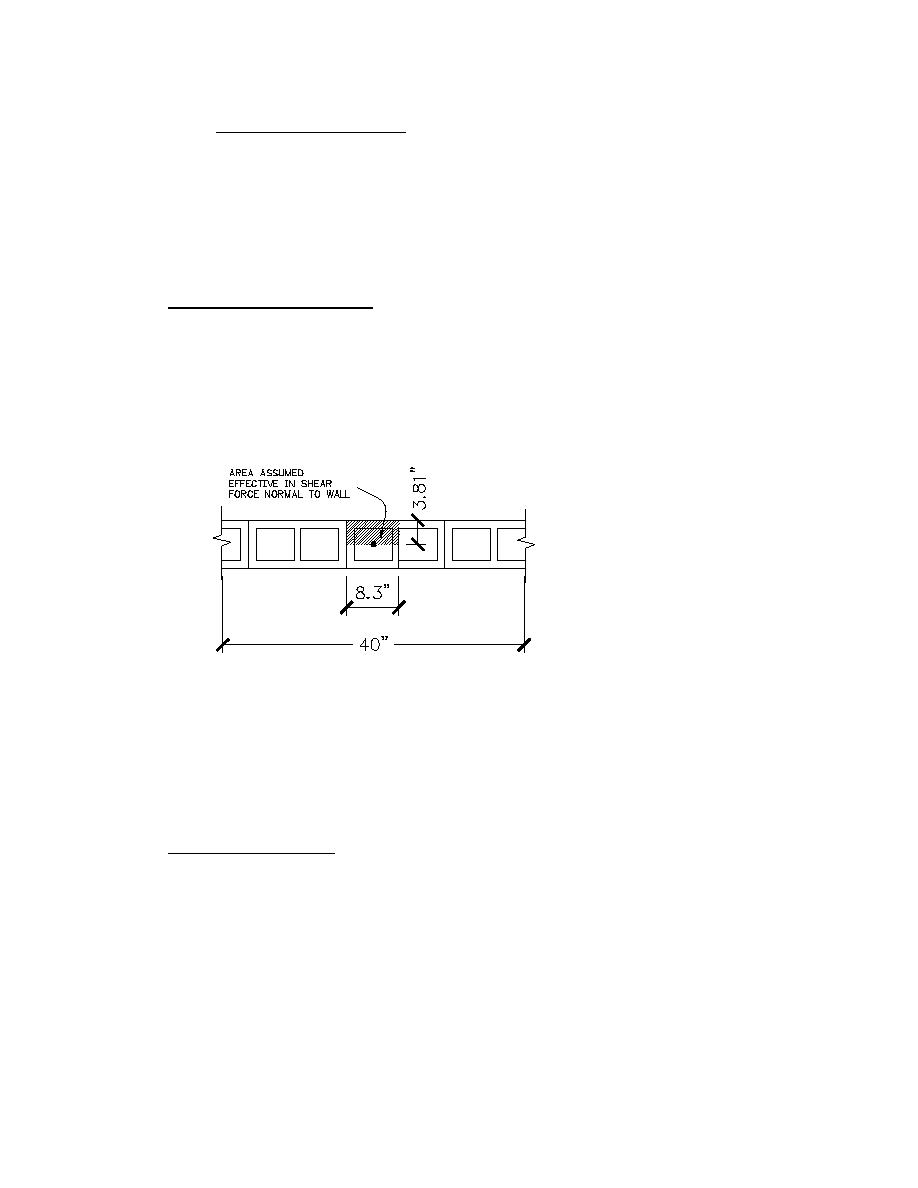
Shear capacity;
Effective shear area, Ae = (8.3")(3.81") = 31.62 in.2 / 40"
(TM 5-809-3 Fig. 5-2)
fv = Ra / bwd , where bwd = Ae and Ra = 547 lb.
(TM 5-809-3 Eq. 6-17)
Fa = 547 lb / 31.62 in.2 = 17.3 psi (119 KN/m2) < 69.7 psi (481 KN/m2), OK
Out-of-plane bracing forces
Anchorage of walls to flexible diaphragms shall have the strength to develop the out-of-plane force give
by:
Fp = 1.2SDSIWp
FEMA 302 Eq. 5.2.6.3.3
-
Interior wall E1-E2
Wp = (57psf)(20'2) = 570 plf (8.32 KN/m)
/
Fp = 1.2(0.6)(1.0)(570) = 410 plf Equivalent to 0.41 ( 40 / 12 ) = 1.37 kips / 40" (5.98 KN/m)
Minimum anchorage demand = 200 plf (2.92 KN/m) < 410 plf (5.98KN/m) (Per Sec. 7-2.e(2))
H1-45



 Previous Page
Previous Page
