AsD = (9.28 kft)(12"/' / (32 ksi)(0.9)(120") = 0.03 in2 (19mm2)
)
It is seen from the low shear stress values that the masonry alone can resist the shear forces without the
reinforcement contribution. Therefore, the horizontal reinforcement will be based on the minimum
reinforcement ratio details for all wall piers.
The trim steel requirement for each pier will be satisfied by having 2 - # 6 bars at the edges of openings, at
wall ends, and at control joints.
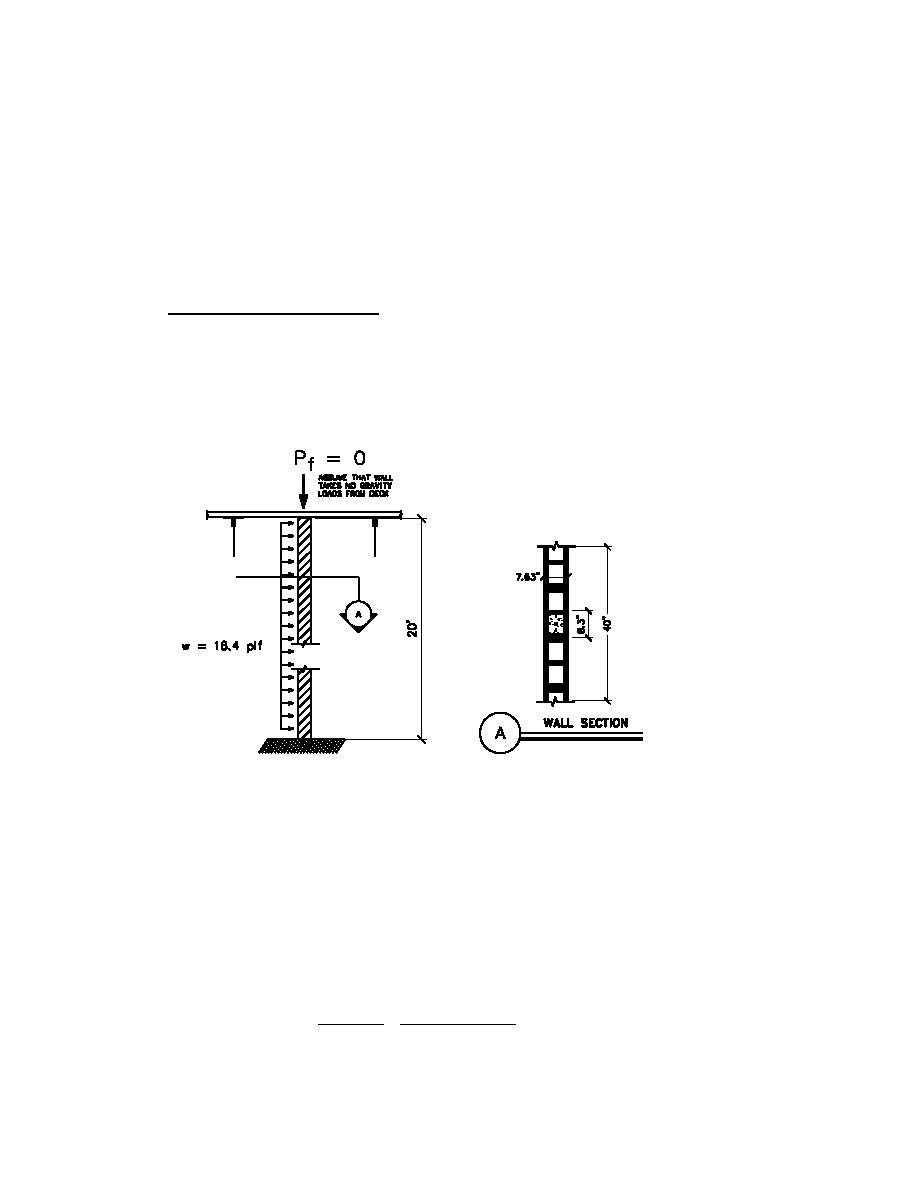
Out-of-plane forces on CMU walls
The CMU walls must be checked for the interaction of axial loads (due to self-weight) and flexural
moments. Wall E1-E2 is the most critical of the walls due to its slenderness and long unbraced height
(20' . For walls with h/tw > 24 it is suggested that the moment magnification due to P-∆ effects be
)
considered (TM 5-809-3 Section 6-5). Wall E1-E2 has h/tw = 240"/8" = 30 > 24, include P-∆ effects.
Determine out-of-wall strength:
1 plf = 14.59 N/m
1 inch = 25.4 mm
- Assume #6 bar at 40" o/c
- f' = 1500 psi (10.3 N/mm2), Fm = 1/3 f' * (1.33) = 1/3(1500)(1.33) = 665 psi (4.6 N/mm2)
m
m
- Em = 1125 ksi * (7.76 KN/mm2)
- fy = 60 ksi (414 N/mm2), Fs = 24 ksi (165 N/mm2), Es =29000 ksi (200 KN/mm2)
- n = Es / Em = 29000 / 1125 = 25.7 (where n is the modular ratio)
*Note: The elastic modulus used for the out-of-plane deflections (1125 ksi) is determined from the
m
calculation. The use of a lower modulus of elasticity for out-of-plane wall forces is conservative.
Pw = Weight of the wall at mid-height = (57psf)(10 ft.)(40/12) = 1900 lb. / 40"
P + w (10' ) 1.9k + (0.0164)(10)
= 65.3psi (450 KN/m2) (TM 5-809-3 Eq. 6-10)
Axial Load Check: f a =
=
Ae
31.62
H1-42



 Previous Page
Previous Page
