wu = Flong/L =3.15k/30'= 105plf (1.53KN/m)
Lateral load:
w u L2 105plf (30' )2
= 11,813ft - lbs (16.02KN-m)
Mu =
=
Diaphragm moment:
8
8
M u 11,813ft - lbs
T=C=
=
= 394 - lb (1.75KN)
Chord forces:
d
30'
Reactions on braced frames:
Both side frames; RA =RB = wux(tributary length) = 105plf(15' = 1,575-lb (7.01KN)
)
Unit shear:
v = R/d = 1,575-lb/30'= 52.5plf (0.67KN/m)
Drag strut forces:
Tdrag = Cdrag = R/2 = 1,575-lb/2 = 788-lb (3.51KN)
Second Floor Level
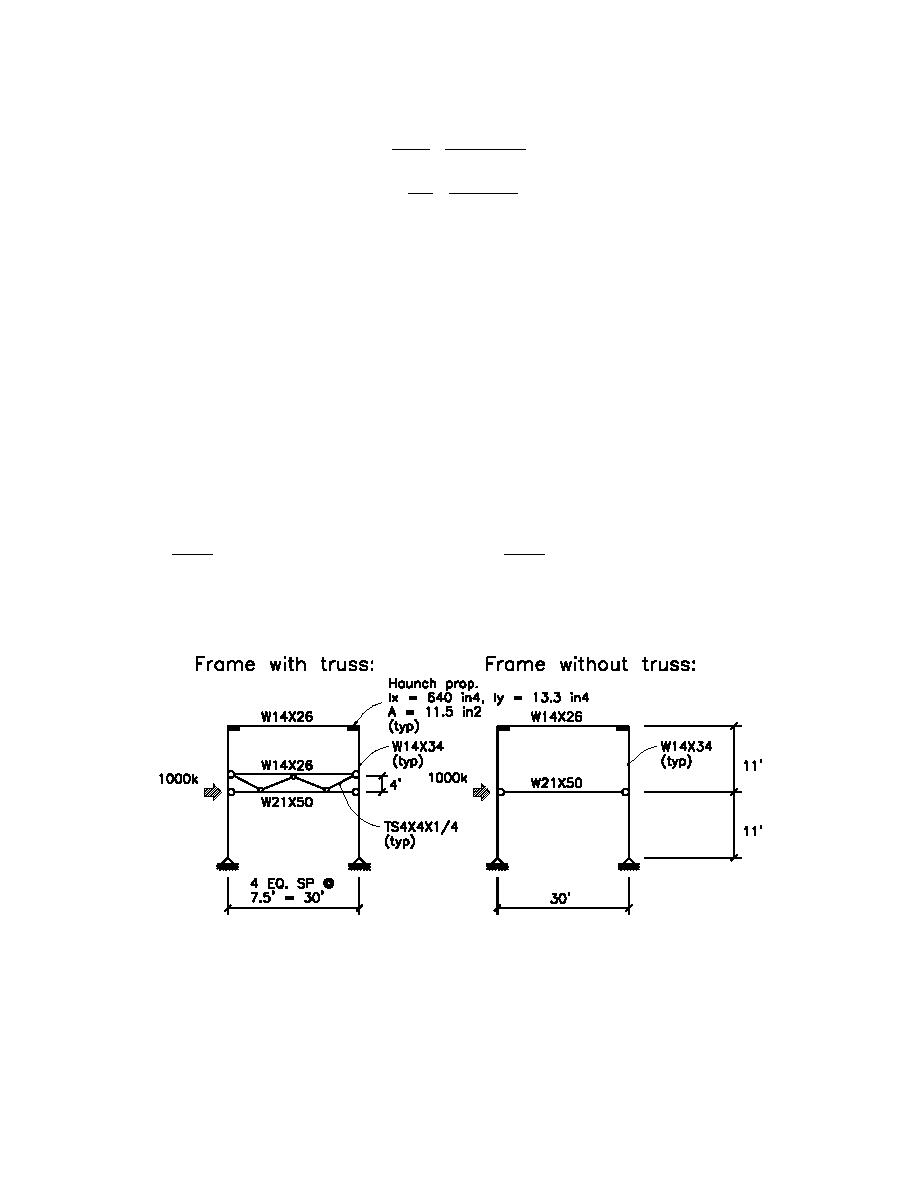
Note: The relative rigidities of the vertical lateral load resisting elements must be determined in order to
establish the distribution of seismic loads. The transverse moment frames were analyzed using a two-
dimensional computer analysis program (RISA-2D, version 4.0) to determine their stiffness. The size of
the braces, in the moment frame at the interface between the high and low roof structures, was assumed, as
they have not yet been designed. The following diagram shows the computer model input and results.
Haunch properties are calculated as shown below. The deflection `∆ ' was taken at the point of applied
loading.
Frame with truss;
Frame without truss;
∆ 3 = 63.9" (1.62X103 mm)
∆ 4,5 = 216" (5.49X103 mm)
1000k
1000k
= 15.7 k /in (2.75KN/mm)
= 4.63k /in (0.81KN/mm)
K3 =
=
K 4,5
63.9"
216"
1-in = 25.4mm
1-ft = 0.30m
1-in = 645.2 mm2
2
1-in4 = 416.2X103 mm4
1-kip = 4.448KN
H4-15



 Previous Page
Previous Page
