TM 5-820-3/AFM 88-5, Chap. 3
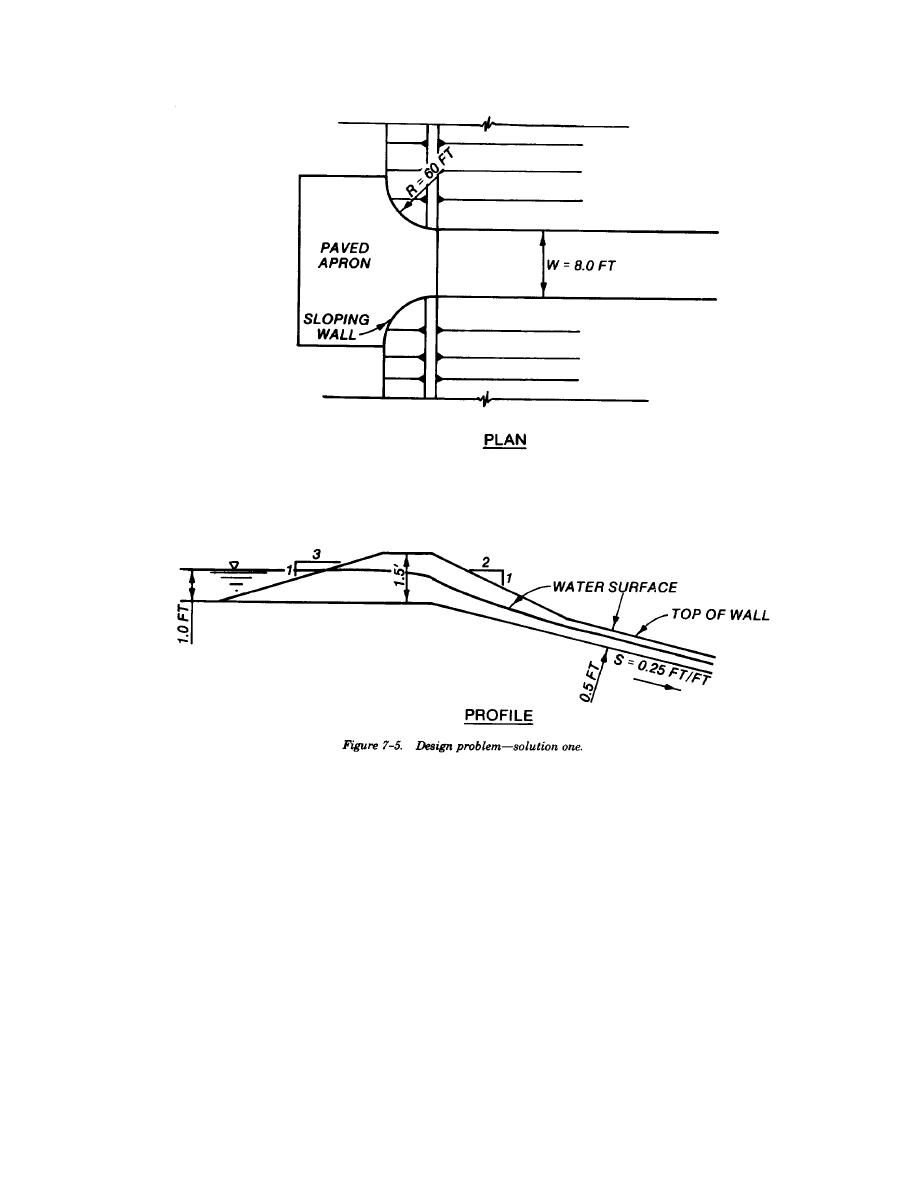
c. Solution two. A drop will he provided at the
Manning's equation (7-2) to determine depth of
entrance. Therefore, a width of chute can he se-
water as in the first solution, find dw=0.493 foot.
lected and the appropriate length and depth of drop
From figure 7-4, with q equals 12.5, sine of angle
determined from the curves in figure 7-3. For this
of slope equals 0.243 and dw equals 0.493 foot,
design select a width of 2 feet. Then H/W = =
determine the depth of air to be 0.311 foot. Thus,
0.5 and Q/W5/2 = 25/(2)5/2 = 4.42. From figure 7-3
total depth is 0.804 foot. Use 0.80 foot. Wall
find a curve that matches these values. This is
height is 1.5 times 0.80 foot, or 1.20 feet. This
found on the curve for D/w 1.0, on the chart for
design is shown in figure 7-6.
B/W=4. Therefore, B=8 feet and D=2.0 feet. Using
7-7



 Previous Page
Previous Page
