TM 5-818-1 / AFM 88-3, Chap. 7
G = ρVs
2
(1) A problem in using seismic methods to
(17-19)
obtain elastic properties is that any induced elastic pulse
where
ρ
(blast, impact, etc.) develops three wave types previously
=
y/32.2 = mass density of soil using
discussed, i.e., P-, S-, and R-waves. Because the
wet or total unit weight
velocity of all seismic waves is hundreds of feet per
Vs =
S-wave velocity (or R-wave), feet per
second and the pickup unit detects all three wave pulses
second
plus any random noise, considerable expertise is
This equation is independent of Poisson's ratio. The Vs
required to differentiate between the time of arrival of the
value is taken as representative to a depth of
wave of interest and the other waves. The R-wave is
approximately one-half wavelength. Alternatively, the
usually easier to identify (being slower, it arrives last;
shear modulus can be computed from the P-wave
traveling near the surface, it contains more relative
velocity and Poisson's ratio from:
energy). Because R- and S-wave velocities are relatively
p( 1 - 2)Vp
2
(17-20)
G=
close, the velocity of the R-wave is frequently used in
2(1- )
computations for elastic properties.
The use of this equation is somewhat limited because
(2) Because amplitudes in seismic survey
the velocity of a P-wave in water is approximately 5000
are very small, the computed shear and Young's moduli
feet per second (approximately the velocity in many
are considerably larger than those obtained from
soils) and Poisson's ratio must be estimated. For
conventional laboratory compression tests.
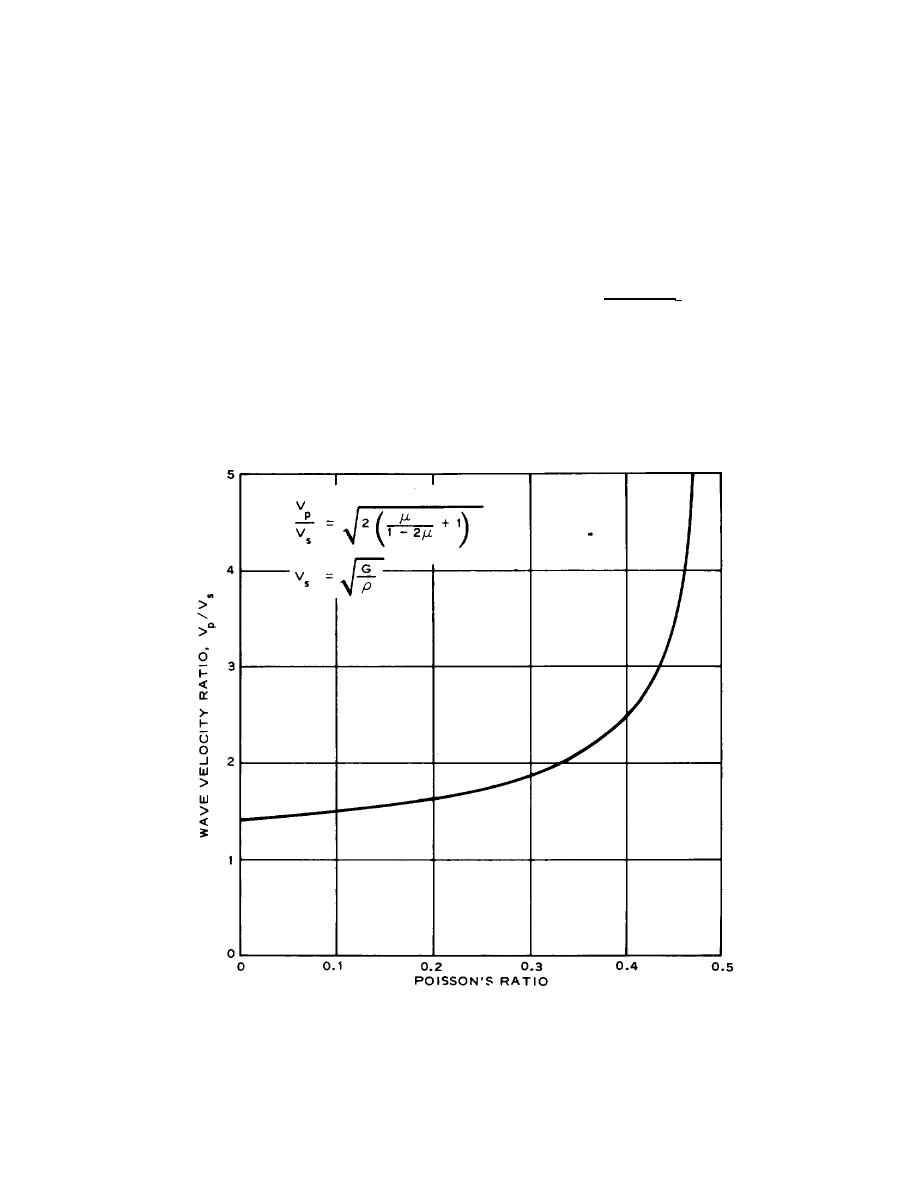
saturated or near saturated soils, - 0.5. The theoretical
(3) The shear modulus, G, may be
variation of the ratio Vs/Vp with is shown in figure 17-8.
calculated from the S- (approximately the R-wave) wave
velocity as follows:
U. S. Army Corps of Engineers
Figure 17-8. Theoretical relation between shear velocity ratio Vp/Vs and Poisson's ratio.
17-11



 Previous Page
Previous Page
