TM 5-818-1 / AFM 88-3, Chap. 7
where
17-3.
Foundations on elastic soils.
a. Foundations on elastic half-space. For very
me = the total rotating mass
small deformations, assume soils to be elastic materials
e = the eccentricity
with properties as noted in paragraph 3-8. Therefore,
theories describing the behavior of rigid foundations
second
resting on the surface of a semi-infinite, homogeneous,
isotropic elastic body have been found useful for study of
e. The ordinate Mz. (fig 17-2(b)) relates the
the response of real footings on soils. The theoretical
dynamic displacement, Az, to me e/m. The peak value of
treatment involves a circular foundation of radius, ro, on
the response curve is a function of the damping ratio and
the surface of the ideal half-space. This foundation has
is given by the following expression:
six degrees of freedom: (1-3) translation in the vertical
1
(z) or in either of two horizontal (x and y) directions; (4)
Mz(max) or Mz = 2D√1-D
2
torsional (yawing) rotation about the vertical (z) axis; or
(17-4)
(5-6) rocking (pitching) rotation about either of the two
horizontal (x and y) axes. These vibratory motions are
For small values of D, this expression becomes 1/2D.
illustrated in figure 17-3.
These peak values occur at frequency ratios of
(1) A significant parameter in evaluating
fo
fn=√1-D
2
the dynamic response in each type of motion is the
(fig. 17-2a)
inertia reaction of the foundation. For translation, this is
or
(17-5)
simply the mass, m = (W/g); whereas in the rotational
1
fo
fn= √1-2D
2
(fig. 17-2b)
(Courtesy) of F. E Richart, Jr., J R. Hall. Jr., and R. D.
Woods, Vibrations of Soils and Foundations, 1970, p 316.
Reprinted by permission of Prentice-Hall, Inc., Englewood
Cliffs, N. J.)
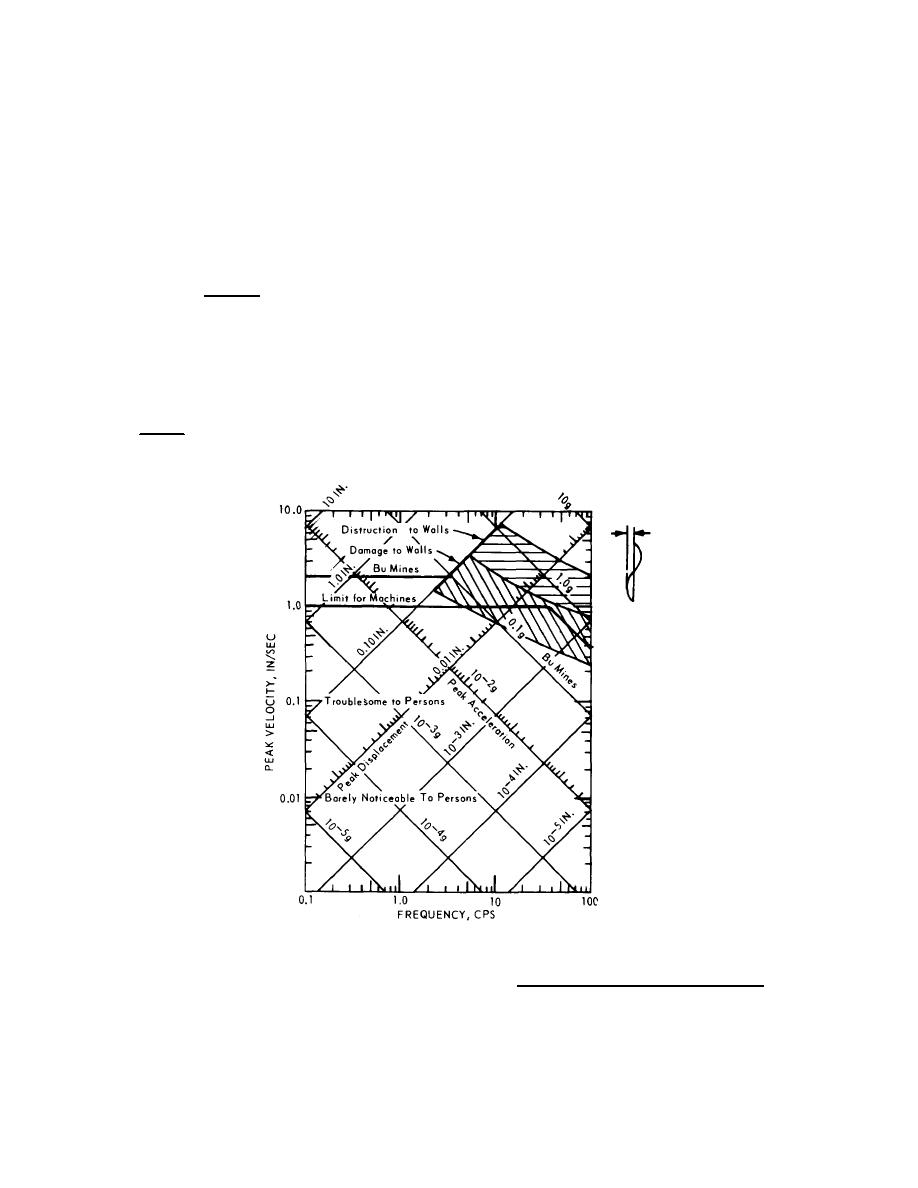
Figure 17-1. Response spectra for tibraton limits.
17-2



 Previous Page
Previous Page
