1.55 - in2
ρ=
= 0.00395 > 0.00333 = ρmin
O.K.
18" (21.81" )
Check moment strength at face of joint per ACI 318-95 Section 21.3.2.2;
1
1
(φ -n ) @ jo int = (200ft - k ) = 100ft - k < 147 ft - k = (φ +n ) (135.6KN-m < 199.3KN-m)
O.K.
M
M
2
2
Therefore, choose 5 #5 (15M) bottom bars at column face
Positive moment at midspan;
By inspection, the governing load combination is 1(U = 1.4D);
M +u = 1.4(12.5ft - k ) = 17.5ft - k (23.7KN-m)
Due to the load demand at this section, steel will be governed by detailing requirements. By inspection, the
minimum reinforcement requirements of ACI 318-95 Section 10.5, and 21.3.2.1 will govern. Since the
steel at the column face is very close to the minimum, it is not possible to terminate any bars.
Check capacity per ACI 318-95 Section 21.3.2.2;
1
1
(φ -n )@ jo int = (200ft - k ) = 50ft - k < 147 ft - k = (φ +n ) (67.8KN-m < 199.3KN-m)
O.K.
M
M
4
4
Check development of positive moment reinforcement at inflection points per ACI 318-95 Section 12.11;
M
ld ≤ n + l a
(EQ. 12-2 ACI 318-95)
Vu
where; Mn = Mu = 147ft-k/0.9 = 163ft-k (221.0KN-m)
Vu; Vu is evaluated at the inflection point as follows;
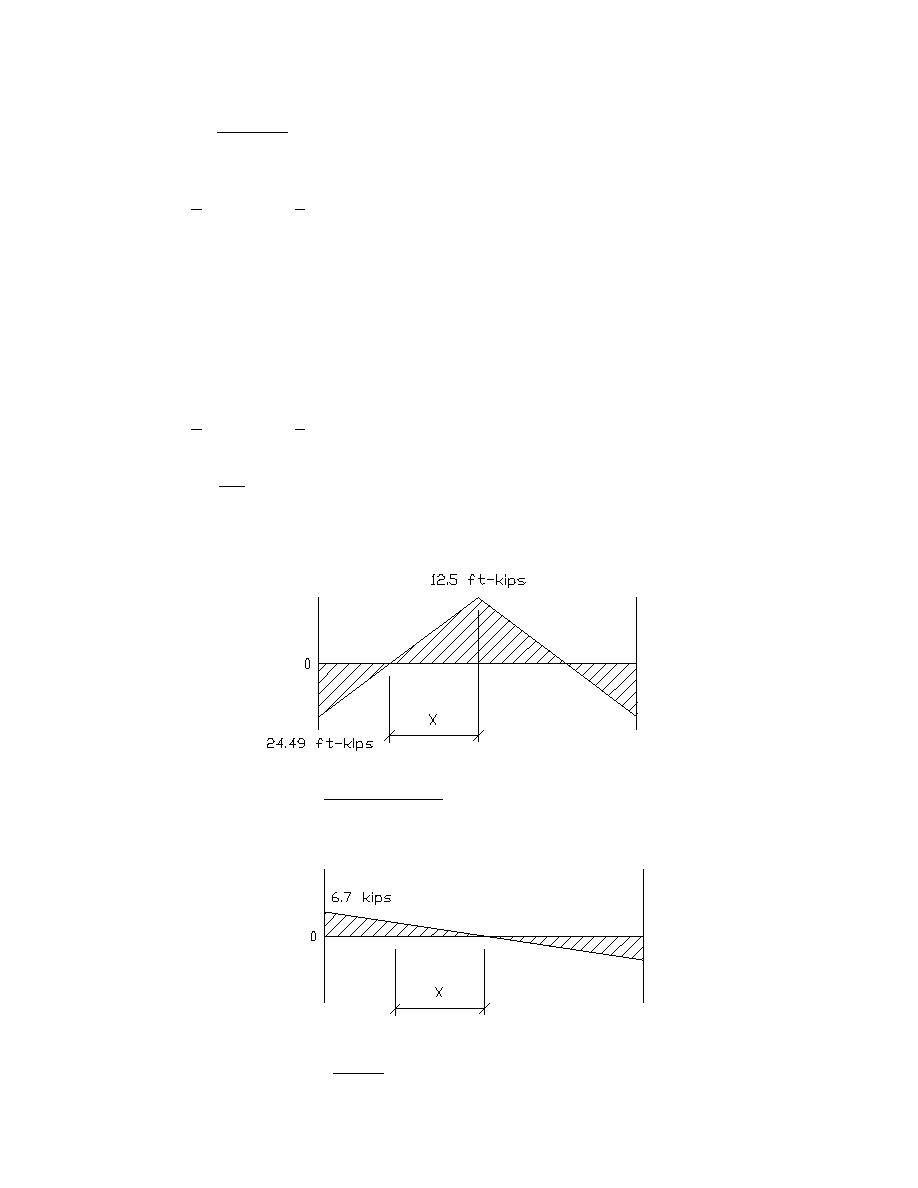
Inflection point is located from the beam centerline using similar triangles;
1-ft-kip = 1.356KN-m
21.5'/2
(12.5ft - k ) = 3.63' (1.11m)
x=
ft - k
ft - k
+ 12.5
(24.5
)
Similarly, Vu is determined at the inflection point;
1-kip = 4.448KN
6.7 k
(3.63' ) = 2.26k (10.05KN)
Vu =
(21.5'/2)
H2-39




 Previous Page
Previous Page
