TM 5-818-1 / AFM 88-3, Chap. 7
motion. These changes are a function of the type of
motion and the embedment ratio d/ro.
(1) For vertical vibrations, both analytical
and experimental results indicate an increase in the
static spring constant with an increase in embedment
depth. Embedment of the circular footing a distance d/ro
< 1.0 produces an increase in the embedded spring
constant kzd' which is greater than kz (table 17-1) by kzd/kz
≅ (1 + 0.6 d/ro). An increase in damping also occurs, i.e.,
Dzd/Dz (1 + 0.6 d/ro). These two approximate relations
lead to an estimate of the reduction in amplitude of
motion because of embedment from Azd / Az = 1 / Dzd / Dz
x kzd/kz). This amount of amplitude reduction requires
complete soil adhesion at the vertical face, and test data
have often indicated less effect of embedment. Test
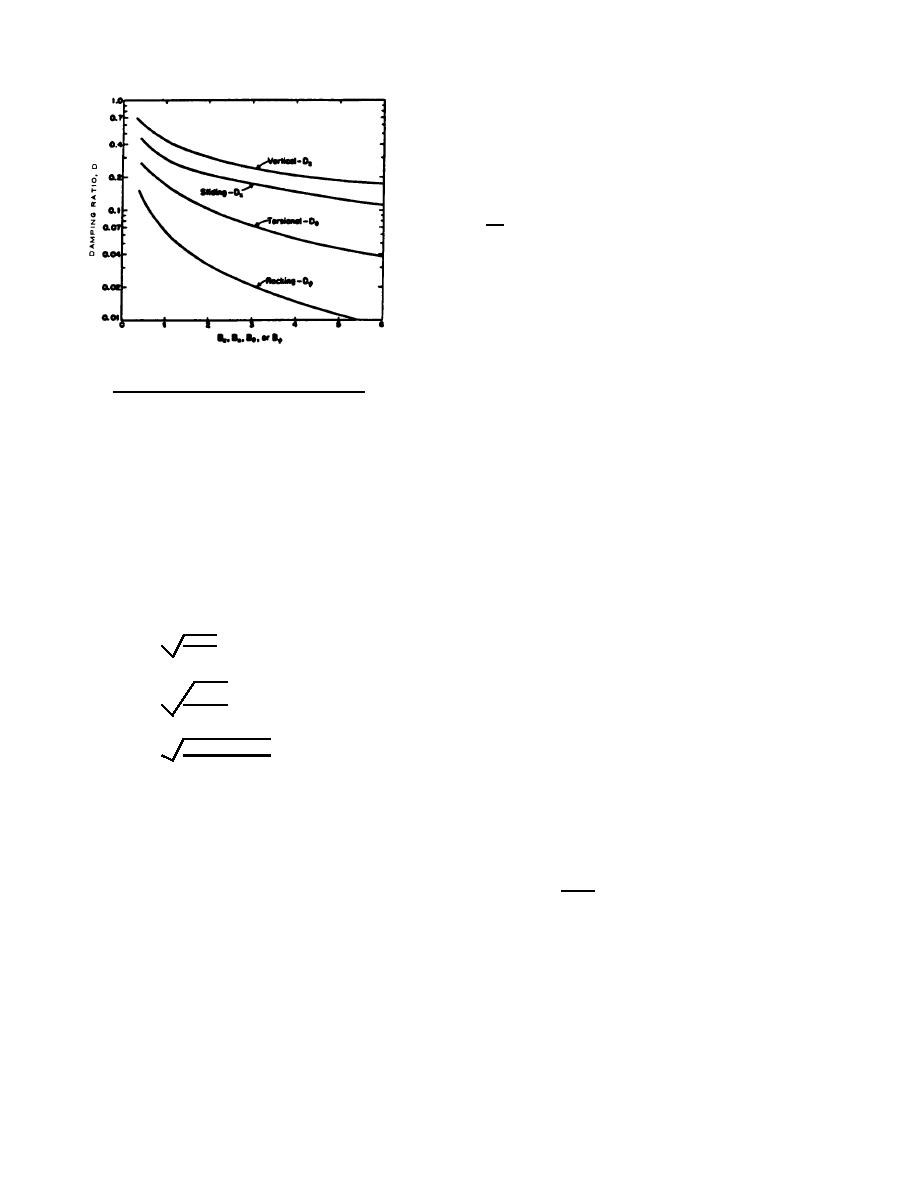
(Courtesy of F. E. Richart, Jr. J. R. Hall, Jr., and R. D.
data indicate that the resonant frequency may be
Woods, Vibrations of Soils and Foundations, 1970. p
increased by a factor up to (1 + 0.25 d/ro) because of
226. Reprinted by permission of Prentice-Hall, Inc.,
embedment.
Englewood Cliffs, N. J.)
(2) The influence of embedment on
coupled rocking and sliding vibrations depends on the
Figure 17-4. Equivalent damping ratio for oscillation of
ratio Bω/Bx (table 17-1). For Bω/Bx ≅ 3.0, the increase in
rigid circular footing on elastic half-space.
natural frequency due to embedment may be as much as
(1 + 0.5 d/ro). The decrease in amplitude is stongly
b. Effects of shape of foundation.
The
dependent upon the soil contact along the vertical face of
theoretical solutions described above treated a rigid
the foundation, and each case should be evaluated on
foundation with a circular contact surface bearing against
the basis of local soil and construction conditions.
the elastic half-space. However, foundations are usually
e. Effect of finite thickness of elastic layer.
rectangular in plan.
Rectangular footings may be
Deposits of real soils are seldom homogeneous to
converted into an equivalent circular footing having a
significant depths; thus theoretical results based on the
radius ro determined by the following expressions:
response of a semi-infinite elastic media must be used
For translation in z- or x-directions:
with caution. When soil layers are relatively thin, with
ro = 4cd
(17-10)
respect to foundation dimensions, modifications to the
π
theoretical half-space analyses must be included.
For rocking:
(1) Generally, the effect of a rigid layer
3
ro =4 16cd
(17-11)
underlying a single elastic layer of thickness, H, is to
3n
reduce the effective damping for a foundation vibrating at
For torsion:
the upper surface of the elastic layer. This condition
2
2
ro =4 16cd(c + d )
(17-12)
results from the reflection of wave energy from the rigid
6π
base back to the foundation and to the elastic medium
In equations (17-10), (17-11), and (17-12), 2c is the
surrounding the foundation. For vertical or torsional
width of the rectangular foundation (along the axis of
vibrations or a rigid circular foundation resting on the
rotation for rocking), and 2d is the length of the
surface of the elastic layer, it has been established that a
foundation (in the plane of rotation for rocking). Two
very large amplitude of resonant vibrations can occur if
values of ro are obtained for rocking about both x and y
axes.
Vs
c. Computations. Figure 17-5 presents
> 4H(17-13)
examples of computations for vertical motions (Example
fo
1) and rocking motions (Example 2).
In equation (17-13), V, is the shear wave velocity in the
d. Effect of embedment.
Embedment of
elastic layer and fo is the frequency of footing vibrations.
foundations a distance d below the soil surface may
When the conditions of equation (17-4) occur, the natural
modify the dynamic response, depending upon the soil-
frequency (equation (17-1)) becomes the important
foundation contact and the magnitude of d. If the soil
design criterion because at that frequen-
shrinks away from the vertical faces of the embedded
foundation, no beneficial effects of embedment may
occur. If the basic evaluation of foundation response is
based on a rigid circular footing (of radius ro) at the
surface, the effects of embedment will cause an increase
17-5




 Previous Page
Previous Page
