TM 5-818-8/AFJMAN 32-1030
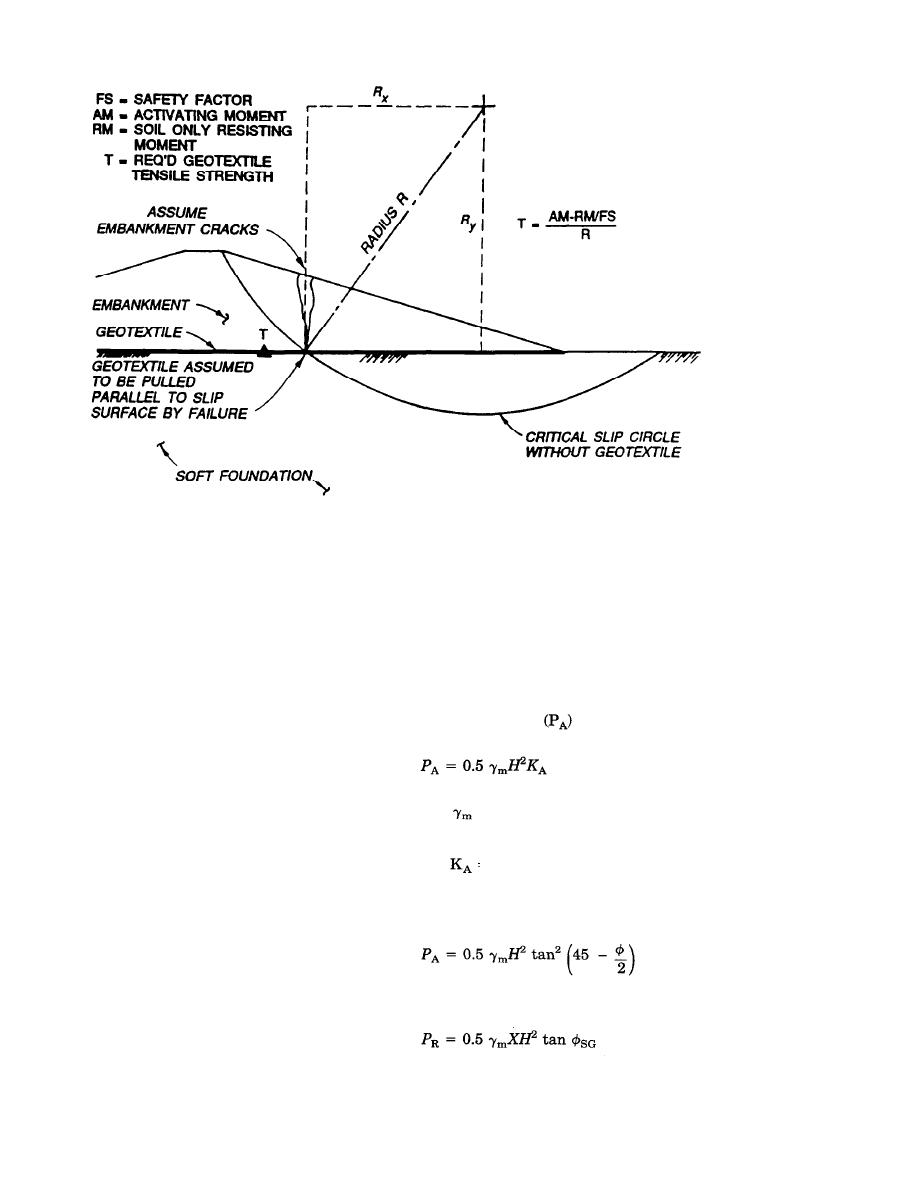
Figure 4-2. Concept Used for Determining Geotextile Tensile Strength Necessary to Prevent Slope Failure.
in figure 4-3. These forces consist of an actuating
(3) The conventional assumption is that criti-
force composed of lateral earth pressure and a
cal slip circles will be the same for both the
resisting force created by frictional resistance be-
geotextile-reinforced and nonreinforced embank-
tween the embankment fill and geotextile. To
ments although theoretically they may be differ-
provide the adequate resistance to sliding failure,
ent. Under these conditions, a stability analysis is
the embankment side slopes may have to be
performed for the no-geotextile condition, and a
adjusted, and a proper value of soil-geotextile
critical slip circle and minimum factor of safety is
friction needs to be selected. Lateral earth pres-
obtained. A driving moment or active moment
sures are maximum beneath the embankment
(AM) and soil resistance moment (RM) are deter-
crest. The resultant of the active earth pressure
mined for each of the critical circles. If the factor
per unit length
for the given cross section
of safety (FS) without geotextile is inadequate,
may be calculated as follows:
then an additional reinforcement resistance mo-
ment can be computed from the following equa-
(eq 4-2)
tion:
where
(eq 4-1)
= embankment fill compacted density-force
TR + RM/FS = AM
per length cubed
where
H = maximum embankment height
T = geotextile tensile strength
= coefficient of active earth pressure (di-
R = radius of critical slip circle
mensionless)
RM = soil resistance moment
FS = factor of safety
For a cohesionless embankment fill, the equation
AM = driving or active moment
becomes:
This equation can be solved for T so that the
(eq 4-3)
geotextile reinforcement can also be determined to
provide the necessary resisting moment and re-
Resistance to sliding may be calculated per unit
quired FS.
length of embankment as follows:
c. Sliding Wedge Analysis. The forces involved
in an analysis for embankment sliding are shown
(eq 4-4)
4-4




 Previous Page
Previous Page
